Python Method Resolution Order and C3 linearization algorithm
Method Resolution Order (MRO) is a order in which methods should be inherited in the case of multiple iheritance. C3 linearization algorithm is how MRO works under the hood since version 2.3.
Wikipedia does a great job explaining the algorithm. It can be reduced to the following steps:
- Linearization (i.e. resolution order) is a class itself and a merge of the linearizations of its parents and a list of the parents itself
- Linearization of the class with no parents equals to the class itself.
- Merge process is done by selecting the first head of the lists which does not appear in the tail of any of the lists. Where head is the first element of the list, and tail is all but first elements of the list. The heads are repeatedly selected and added to the resulting MRO until all the lists are exhausted.
- If a head cannot be selected while not all the lists are exhausted merge is impossible to compute due to inconsistent orderings of dependencies in the inheritance hierarchy and no linearization of the original class exists.
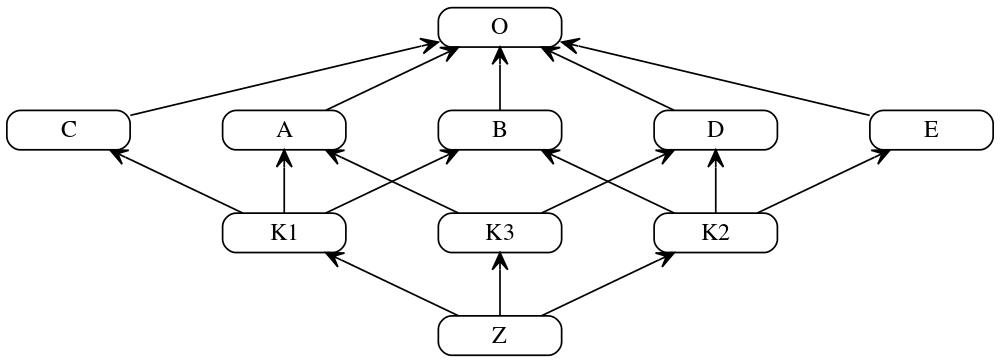
Complex multiple inheritance example, courtesy H2power
Consider linearization process for a class K1:
// first, find the linearizations of K1's parents, L(A), L(B), and L(C),
// and merge them with the parent list [A, B, C]
L(K1) := [K1] + merge(L(A), L(B), L(C), [A, B, C])
// class A is a good candidate for the first merge step, because it only
// appears as the head of the first and last lists
= [K1] + merge([A, O], [B, O], [C, O], [A, B, C])
// class O is not a good candidate for the next merge step, because it also
// appears in the tails of list 2 and 3; but class B is a good candidate
= [K1, A] + merge([O], [B, O], [C, O], [B, C])
// class C is a good candidate; class O still appears in the tail of list 3
= [K1, A, B] + merge([O], [O], [C, O], [C])
// finally, class O is a valid candidate, which also exhausts all remaining lists
= [K1, A, B, C] + merge([O], [O], [O])
= [K1, A, B, C, O]
So at the higher level a naive implementation of the C3 linearization algorith can be expressed as a simple recursion:
def mro(cls: type) -> List[type]:
"""
Return a list of classes in order corresponding to Python's MRO.
"""
result = [cls]
if not cls.__bases__:
return result
else:
return result + _merge(*[mro(kls) for kls in cls.__bases__], cls.__bases__)
Then _merge repeatedly checks if its lists are exhausted and append appropriate heads to the resulting MRO:
def _merge(*lists) -> list:
result: List[Optional[type]] = []
linearizations = DependencyList(*lists)
while True:
if linearizations.exhausted:
return result
for head in linearizations.heads:
if head and (head not in linearizations.tails): # type: ignore
result.append(head)
linearizations.remove(head)
# Once candidate is found, continue iteration
# from the first element of the list
break
else:
# Loop never broke, no linearization could possibly be found
raise ValueError('Cannot compute linearization, a cycle found')
In order to hide some lists internals Dependency and DependencyList abstractions are used:
from collections import deque
from itertools import islice
from typing import List, Tuple, Optional
class Dependency(deque):
@property
def head(self) -> Optional[type]:
try:
return self[0]
except IndexError:
return None
@property
def tail(self) -> islice: # type: ignore
"""
Return islice object, which is suffice for iteration or calling `in`
"""
try:
return islice(self, 1, self.__len__())
except (ValueError, IndexError):
return islice([], 0, 0)
class DependencyList:
"""
A class represents list of linearizations (dependencies)
The last element of DependencyList is a list of parents.
It's needed to the merge process preserves the local
precedence order of direct parent classes.
"""
def __init__(self, *lists: Tuple[List[type]]) -> None:
self._lists = [Dependency(i) for i in lists]
def __contains__(self, item: type) -> bool:
"""
Return True if any linearization's tail contains an item
"""
return any([item in l.tail for l in self._lists]) # type: ignore
def __len__(self):
size = len(self._lists)
return (size - 1) if size else 0
def __repr__(self):
return self._lists.__repr__()
@property
def heads(self) -> List[Optional[type]]:
return [h.head for h in self._lists]
@property
def tails(self) -> 'DependencyList': # type: ignore
"""
Return self so that __contains__ could be called
Used for readability reasons only
"""
return self
@property
def exhausted(self) -> bool:
"""
Return True if all elements of the lists are exhausted
"""
return all(map(lambda x: len(x) == 0, self._lists))
def remove(self, item: Optional[type]) -> None:
"""
Remove an item from the lists
Once an item removed from heads, the leftmost elements of the tails
get promoted to become the new heads.
"""
for i in self._lists:
if i and i.head == item:
i.popleft()
The whole codebase can be found in my c3linear repository. You can install it from the source code or via PyPI:
python setup.py install # from the source code
pip install c3linear # from the Cheese Shop
Then just import it and check against Python’s object’s mro method:
from c3linear.mro import mro
class A: pass
class B(A): pass
mro(B) == B.mro()
Take a look at the tests to dive into more complex multiple inheritance examples.